
Угол между плоскостями.
Date: 2015-10-07; view: 473.
Вопросы к тесту.
1.На комплексной плоскости к.ч.  изображается:
изображается:
Точкой, z=x+iy , Im – мнимая точка, Re – действительная z(x;y), x=ReZ, y=ImZ
2.Для комплексного числа  показательная форма записи имеет вид:
показательная форма записи имеет вид:
z=ρ*e^i*φ
3.Для комплексного числа  произведение
произведение  равно:
равно:
 =(x+iy)(x-iy)=x^2+y^2= ρ^2 , где z(штрих) – сопряженное число
=(x+iy)(x-iy)=x^2+y^2= ρ^2 , где z(штрих) – сопряженное число
4.Формула Эйлера имеет вид: cos φ+isin φ=e^iφ
5.Вычислить Модуль к.ч |z|= ρ= (x^2+y^2)^1/2 , 0<= ρ<+∞
6.Вычислить Аргумент к.ч.
z= ρ(cos φ+isin φ) , φ- аргумент к.ч. , φ=Argz+2πk ,
arctg y/x , x>0
φ = π + arctg y/x , x<0, y>=0 где 0<= φ<=2 π или - π<= φ<=π
- π + arctg y/x , x<0 , y<0
7.Если  возвести в квадрат, то получится:
возвести в квадрат, то получится:
z^n= ρ^n(cos φ+isin φ) => z^α = ρ^α(cos φ+isin φ)
8.Сколько корней имеет алгебраическое уравнение
1-н корень – действительный или комплексный(основная теорема алгебры)
9.Вектор  , построенный на (..)
, построенный на (..)  и
и  , имеет координаты:
, имеет координаты:
M(x1,y1,z1)
ð  (x2-x1,y2-y1,z2-z1)
(x2-x1,y2-y1,z2-z1)
N(x2,y2,z2)
10.Модуль вектора  равен:
равен:
Модулем или длиной вектора а называют расстояние между его началом и концами
Если вектор а=(  ;
;  ;
;  ), то |
), то |  | =
| = 
11.Вектор ортогональный к  имеет координаты
имеет координаты
12.Сумма векторов 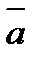 и
и  равна:
равна:
 +
+  =
=  ; суммой векторов
; суммой векторов 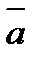 и
и  называется вектор
называется вектор  , начало которого находится в начале вектора
, начало которого находится в начале вектора  , а конец в конце
, а конец в конце 
13.Если  и
и  , то
, то  равно:
равно:
При умножении вектора на число его координата * на это число
 =(
=(  *
*  ;
;  *
*  ;
;  *
*  )
)
14.В каком из выражений результатом является вектор?
15.Скалярное произведение векторов  и
и  равно:
равно:
1.  *
*  =|
=|  |*|
|*|  |*cos(
|*cos(  угол между ними
угол между ними  )
)
2.  *
*  =|
=|  |*
|*  =|
=|  |*
|* 
3.  *
*  =
= 
16.Векторное произведение векторов  и
и  равно:
равно:
Векторным произведением векторов  и
и  называется вектор
называется вектор  , обозначаемый
, обозначаемый  =
=  x
x  =[
=[  ,
,  ] и удовлетворяющий 3-м свойствам: 1. Модуль вектора с = площади параллелограмма, построенного на векторах а и b. |
] и удовлетворяющий 3-м свойствам: 1. Модуль вектора с = площади параллелограмма, построенного на векторах а и b. |  | =|
| =|  |*|
|*|  |*sin(
|*sin(  угол между ними
угол между ними  )=S . 2.
)=S . 2. 

 и
и 

 =>
=> 
 плоскости
плоскости 
 .
.
17.Векторы  компланарны, если равно нулю их:
компланарны, если равно нулю их:
Векторное произведение
18.При умножении матриц  на
на  получается: С=A*B посчитать
получается: С=A*B посчитать
19.При сложении матриц  и
и  получается: C=A+B посчитать
получается: C=A+B посчитать
20.Для невырожденной матрицы обратная матрица имеет вид
∆=detA≠0 невырожденая матрица
∆=detA=0 вырожденая матрица
A^-1=(1/detA)*[  ]^T
]^T
21.Какое из свойств матриц справедливо?
Если произвольную матрицу A умножить слева или справа на единичную матрицу, то в результате получится исходная матрица: E*A=A*E=A
22.Какое из свойств справедливо для обратной матрицы?
Свойства: обратной матрицы:
1. Det(A^-1)=1/detA
2. (A*B)^-1=B^-1*A^-1
3. (A^-1)^T=(A^T)^-1
A*(A^-1)= (A^-1)*A=E
23.Определитель матрицы равен: разнице произведений элементов главной диагонали и побочной
24.Какое из свойств справедливо для определителя: св-во равноправия строк и столбцов ∆А=∆А^T A=  A^T=
A^T= 
25.разложение определителя по строке(столбцу) имеет вид:
det  =
=  *
*  =
=  *
*  – по строке
– по строке
det  =
=  *
*  =
=  *
*  – по столбцу
– по столбцу
26.Понятие подпространства, линейного оператора
Непустое подмножество U линейного пространства V наз. подпространством, если x+y ϵ U для любых векторов x,y ϵ V и α, β ϵ Fвещественные числа
27.Собственные числа и собственные вектора. Как найти
· Собственный вектор – любой ненулевой вектор x, который отображается оператором
· Собственными числами матрицы А являются корни уравнения |A-λE|=0 b и только они
28.Через (.)  и вектор
и вектор  проходит прямая: A(x-x0)+B(y-y0)=0
проходит прямая: A(x-x0)+B(y-y0)=0
29.Через (.)  и вектор
и вектор  проходит прямая: (x-x0)/l=(y-y0)/m – каноническое ур.
проходит прямая: (x-x0)/l=(y-y0)/m – каноническое ур.
30.Уравнения прямой на плоскости. Ax+By+c=0
31.В какой точке пересекаются прямые:
A1x+B1y+C1=0
A2+B2y+C2=0
32.Угловой коэффициент прямой равен:
tg φ=(k2-k1)/(1+k2*k1)
если прямые || => k1=k2
если прямые  => k1=-1/k2
=> k1=-1/k2
33.Расстояние от точки до прямой вычисляется:
L:Ax+By+C=0 и т. M0(x0;y0), вектор n (A;B)
d= 
34.Расстояние между скрещивающимися прямыми задается формулой:
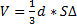


35.Как расположены прямые: прямые не лежат в одной плоскости
36.Отрезки, отсекаемые прямой на координатных осях, равны:

a-отрезок, который отсекает прямая от оси Ох
b- отрезок, который отсек. прямая от корд. оси OY
37.Какое из уравнения задает прямую в пространстве?

Прямую можно задать либо 2-мя уравнениями плоскостей, либо пучком плоскостей, проходящих через эту прямую:

38.Какое из уравнений задает плоскость?

39.Уравнение плоскости в отрезках имеет вид:

40.Условие параллельности прямой  и плоскости
и плоскости  задается условием:
задается условием:
 ,
,  , Al+Bm+Cn=0,
, Al+Bm+Cn=0, 
41.Угол между прямой и плоскостью определяется формулой:


 o-α
o-α

42.Сколько направляющих (коллинеарных) векторов имеет плоскость:
43.Сколько различных направляющих векторов имеет плоскость:
44.Расстояние от точки до плоскости:

угол между плоскостями можно определить как угол между их направляющими векторами  и
и 

Если K1||K2, то и  =>
=> 
Если K1 перпендикулярен K2 , то φ=90 => A1A2+B1B2+C1C2=0
46.Через (.)  и вектор
и вектор  проходит плоскость:
проходит плоскость:
A(x-x0)+B(y-y0)+C(z-z0)+D=0
47.Какое уравнение кривой задают условия: 

48.Найти расстояние между фокусами если известно 

49.В уравнении Гиперболы (Эллипса) константа  называется:
называется:
большой осью
50.Какое уравнение кривой задается параметром  :
:
 уравнение директрисы (2 замечат. кривые перпендикуль. большой оси)
уравнение директрисы (2 замечат. кривые перпендикуль. большой оси)
51.Метод Крамера задается формулами:


52.Решение СЛАУ методом Гаусса, матричным, Крамера
1. Гаусса: сводим матрицу к треуг. виду, обратным ходом определяем неизвестные
2. Матричный метод: 
3. Крамера: detA= 






53.Общее решение неоднородной СЛАУ
Решение определяется формулой 
54.Для матрицы выражение  равно:
равно:
Алгебраическое дополнение:  , где Mij -получаемый из основного определителя вычёркиванием из него i-ой строки и j-го столбца.
, где Mij -получаемый из основного определителя вычёркиванием из него i-ой строки и j-го столбца.
55.Рангом матрицы называется:
порядок базисного минора. В матрице A mxn минор порядка r называется базисным, если он отличен от (M^r≠)
56.Чем линейное пространство отличается от векторного
57.Найти параметр параболы:
Например: 
58.Какую из поверхностей задает уравнение:
59.Парабола (гипербола, эллипс) задается уравнением:
Каноническое уравнение эллипса:  E<1
E<1
Гипербола  =1 E<1
=1 E<1
Парабола:  E=1
E=1
60.Основные характеристики линий второго порядка
1.Окружность: 
2. Эллипс: 

уравнение директрис: 

фокальный параметр: 
3. Гипербола: 
 >1
>1
уравнение директрис: 

фокальный параметр: 
4. Парабола: 
уравнение директрис: x= 
E=1
| <== previous lecture | | | next lecture ==> |
| История религий Дальнего Востока | | | Morphologie und Syntax |