
Линейные операции над векторами (сложение, вычитание, умножение на скаляр; свойства линейных операций).
Date: 2015-10-07; view: 424.
Теорема
Для того чтобы однородная система n-линейных уравнений с m-неизвестными имела не 0-ое решение,необходимо и достаточно,чтобы её определитель был равен 0,то есть 
Если определитель равен 0,это значит,что ранг основной матрицы системы меньше числа неизвестных и значит,что система имеет бесконечное множество решений,то есть имеет и не 0-ое решени
Сложение векторов. Пусть  и
и  – два произвольных вектора. Возьмем произвольную точку О и построим вектор
– два произвольных вектора. Возьмем произвольную точку О и построим вектор  ; затем от точки А отложим вектор
; затем от точки А отложим вектор  . Вектор
. Вектор  , соединяющий начало первого слагаемого вектора с концом второго, называется суммой этих векторов и обозначается
, соединяющий начало первого слагаемого вектора с концом второго, называется суммой этих векторов и обозначается  (рис. 1).
(рис. 1).

Рис. 1
Ту же сумму можно получить иным способом. Отложим от точки О векторы  и
и  . Построим на этих векторах как на сторонах параллелограмм ОАСВ. Вектор
. Построим на этих векторах как на сторонах параллелограмм ОАСВ. Вектор  – диагональ параллелограмма – является суммой векторов
– диагональ параллелограмма – является суммой векторов  и
и  (рис. 2).
(рис. 2).

Рис. 2
Понятие суммы можно обобщить на случай любого конечного числа слагаемых (рис. 3).

Рис. 3
Вычитание векторов.Разностью  векторов
векторов  и
и  называется такой вектор
называется такой вектор  , который в сумме с вектором
, который в сумме с вектором  дает вектор
дает вектор  :
:  Û
Û  .
.
Если векторы  и
и  привести к общему началу, то разность представляет собой отрезок, соединяющий их концы и направленный от «вычитаемого» к «уменьшаемому» (рис. 4).
привести к общему началу, то разность представляет собой отрезок, соединяющий их концы и направленный от «вычитаемого» к «уменьшаемому» (рис. 4).

Рис. 4
Таким образом, если на векторах  и
и  , отложенных из общей точки О, построить параллелограмм ОАСВ, то вектор
, отложенных из общей точки О, построить параллелограмм ОАСВ, то вектор  , совпадающий с одной диагональю, равен сумме
, совпадающий с одной диагональю, равен сумме  , а вектор
, а вектор  , совпадающий с другой диагональю, – разности
, совпадающий с другой диагональю, – разности  (рис. 5).
(рис. 5).

Рис. 5
Умножение вектора на число.Произведением вектора  на действительное число
на действительное число  называется вектор
называется вектор  (обозначают
(обозначают 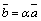 ), определяемый следующими условиями:
), определяемый следующими условиями:
1)  ,
,
2)  при
при 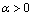 и
и  при
при  .
.
Очевидно, что при 
 .
.
Построим, например, векторы  и
и  для заданного вектора
для заданного вектора  (рис. 6).
(рис. 6).

Рис. 6
Из определения следует: два вектора  и
и  коллинеарны тогда и только тогда, когда имеет место равенство
коллинеарны тогда и только тогда, когда имеет место равенство 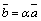 :
:
 (2.1)
(2.1)
Свойства линейных операций:
1)  ;
;
2)  ;
;
3)  ;
;  ;
;
4)  ;
;
5)  ;
;
6)  ;
;
7)  ;
;  ;
;
Пусть дан вектор  . Ортом вектора
. Ортом вектора  (обозначается
(обозначается  ) называется вектор единичной длины, сонаправленный с вектором
) называется вектор единичной длины, сонаправленный с вектором  .
.
Очевидно,  для любого вектора
для любого вектора  .
.
| <== previous lecture | | | next lecture ==> |
| Теорема | | | Линейное (векторное) пространство. |